題目

  • 題目連結
  • 目標函式 : insert(intervals, newInterval)
    • Input : intervals: List[List[int]]、newInterval: List[int]
    • Output : List[List[int]]

解題概念

  • 題意 : 給定一個不重疊的區間 intervals，其中 :
    • intervals[i] = [start_i, end_i] 表示第 i 個區間的開始與結束
    • 區間將會按照 start_i 升序排列
  • 另外也會給定一個區間 newInterval = [start, end]，表示該區間的開始和結束。
  • 將 newInterval 插入 intervals 中，使得 intervals 仍然按 start_i 升序排序，且 intervals 仍然沒有任何重疊區間（如有必要，合併重疊區間）。
  • 需要回傳插入後的 intervals

我的寫法

  • 想法 : 使用 for 迴圈，去判斷 intervals[i] 與 `newInterval 的關係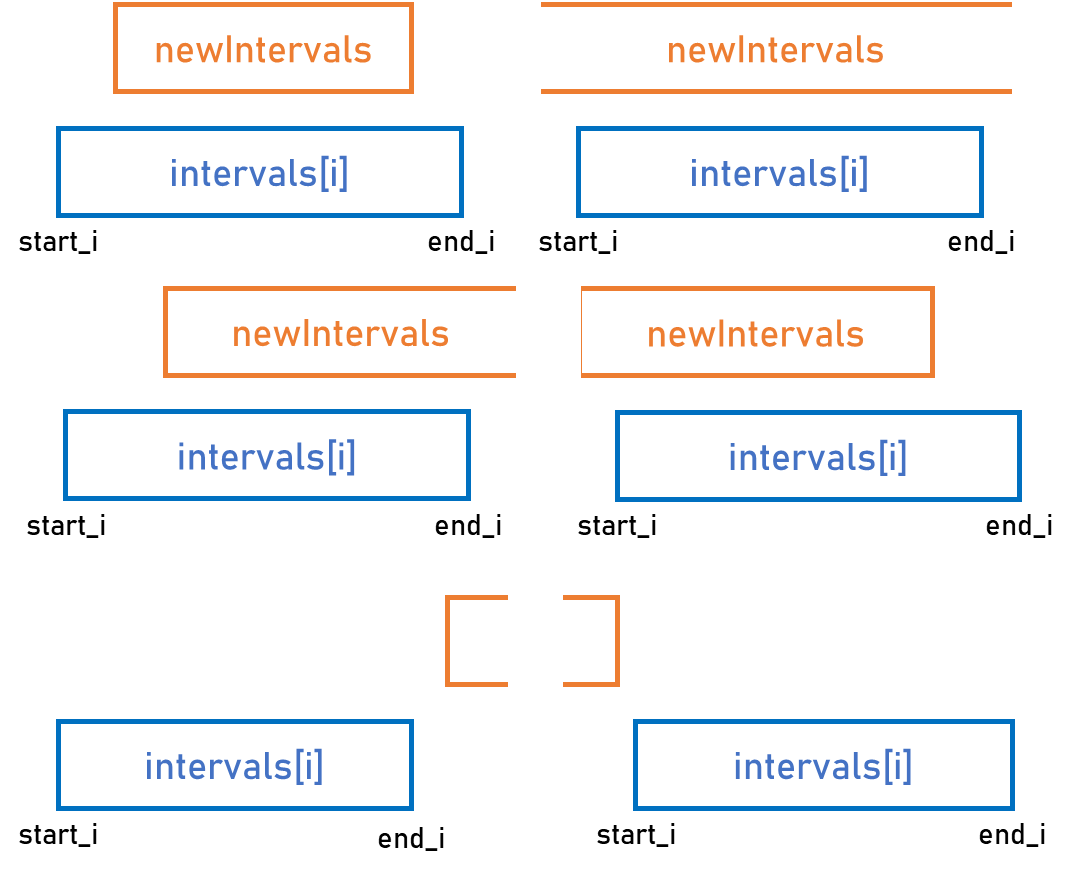

  • 遇到之困難 :

    • 需要判斷這6項狀況以外，還要去判斷每回合的 start[i] 與 end[i] 的去留，這樣在判斷下去會過於複雜…

解答 or 其他優秀寫法

  • 想法 : 其實根本不用思考那6個狀況:O
    • Stage 1 : 若 intervals[i] end 比 newInterval start 還小的話，則一直將 intervals[i] 加到 res 中
    • Stage 2 : 若 intervals[i] start 比 newInterval end 還大 or 相等的話，則合併 intervals[i] 與 newInterval (透過 min() 與 max() 去決定哪個數字要去當新的 start 或 end)，最後在將該值設為新的 newInterval
    • Stage 3 : 此時 intervals[i] 已超出 newInterval 的範圍，故將 newInterval 加到 res 中
    • Stage 4 : 最後將剩下的 intervals[i] 加到 res 中
  • 程式碼 : 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    def insert(self, intervals, newInterval):

        res = []

        i = 0

        # Stage 1
        while i < len(intervals) and intervals[i][1] < newInterval[0]:
            res.append(intervals[i])
            i += 1

        # Stage 2
        while i < len(intervals) and intervals[i][0] <= newInterval[1]:

            new_start = min(newInterval[0], intervals[i][0])
            new_end = max(newInterval[1], intervals[i][1])
            newInterval = [new_start, new_end]
            i += 1
        
        # Stage 3
        res.append(newInterval)

        # Stage 4
        while i < len(intervals):
            res.append(intervals[i])
            i += 1
        
        return res
  • 成效 :
    • Time Complexity : $O(n)$
    • Runtime: 48 ms (faster than 89.49%)
    • Memory Usage: 16.62 MB (more than 72.84%)